티스토리 뷰
Linear Regression(선형 회귀) & Gradient Descent(경사하강법) TensorFlow 1.x, 2.x 반영
lsh424 2020. 2. 6. 13:51오늘은! 머신러닝 모델에서 가장 기본적이고 기초적이라 할 수 있는 선형회귀 모델을 공부해보려 합니다
별로 어렵지 않는내용이면서 재밌게 공부할 수 있어요!
먼저 선형회귀에대해 공부하기 전에, 머신러닝 모델 개발은 다음과 같은 프로세스를 거치게 됩니다.
- 학습하고자 하는 가설(Hypothesis)을 수학적 표현식으로 나타냅니다.
- 가설의 성능을 측정할 수 있는 손실함수(Cost Function 혹은 Loss Function)을 정의합니다.
- 손실함수를 최소화 할 수 있는 알고리즘을 설계합니다.
저는 머신러닝을 공부하기 전에, 도대체 어떻게 컴퓨터가 학습을 하는걸까? 라는 의문을 품고 있었습니다. 이에 대한 답은!! 비용함수(손실함수)를 최소화 하도록 만드는 것이였는데요. 말로만 들어서는 이해가 잘 안가실 수 있지만, 오늘 설명드릴 선형회귀모델을 공부하시고 나면 아! 하실겁니다 ㅎㅎ
혹시 회귀의 의미에 대해 잘 아시나요?, "선형 회귀" 에서 "회귀" 란 간단하게 말해 예측을 말합니다.
선형이라는 말이 붙은 이유는 선형함수를 이용해 회귀를 수행하기 때문인데요.
선형 함수는 다음과 같이 표현할 수 있습니다. y = Wx + b (가설)
여기서 y는 정답 데이터(레이블), x는 인풋 데이터, W,b는 파라미터 입니다.
우리의 목적은 학습을 통해 w,와 b의 값을 바꿔나가면서 데이터를 가장 잘 대변하는 직선의 방정식을 찾는 것 입니다.
cost (혹은 loss)는 가설과 실제 데이터와의 차이라고 할 수 있고, 우리는 이 가설과 실제 데이터의 간극을 줄여나가는 일을 함으로써 w와 b를 바꿔 나갈 수 있습니다. 즉 cost를 minimize(최소화) 하는거죠
다음과 같이 어떤 데이터들이 선형적인 분포를 보인다 했을 때, 이러한 데이터를 가장 잘 대변할 수 있는 y= Wx + b를 찾는 것이 우리의 목표라고 했는데요.
이러한 W와 b를 찾기 위해, 우리는 대표적인 손실함수중 하나인 평균제곱오차(Mean of Squared Error)를 사용하게 됩니다. 줄여서 MSE라 부릅니다.

우리 모델의 예측값 (y hat)과 실제 데이터(y)의 차이가 적을수록 우리가 찾는 정답과 유사한 그래프 일겁니다.
그렇죠? 따라서 실제 데이터와 예측값의 차이의 총합이 줄어드는 방향으로 w와 b의 값을 조절해 나가는 것입니다.
하지만 여기서 문제가 발생합니다. 단순히 빼버리면, 어떤 값은 양수지만 어떤 값은 음수가 나오기 때문에,
다 더했을 때 오류가 생기게 됩니다. 그래서 그 차이를 제곱해버리면 양수가 나오게 되고, 절대적인 차이를 알 수 있게 됩니다. 이러한 절대적인 차이를 줄여나감으로써 w 와 b를 구해나갈 수 있는 것이죠.

이렇게 예측값과 실제 값의 차이의 제곱을 sum 해준 후 y의 개수로 나눠주면 평균제곱 오차 공식이 됩니다.
정말 그런지 확인해 보자구요! , 정답이 y = [1, 10, 13, 7] , 예측값 y^ = [10, 3, 1, 4]이라 했을 때는
MSE = 70.75
정답이 y = [1, 10, 13, 7] , 예측값 y^ = [2, 10, 11, 6]이라 했을 때는
MSE = 1.5
가 나오게 됩니다. 실제로 평균제곱오차 MSE가 클 때보다 적을 때 실제 값과 예측값이 근사한 값을 갖게 되죠?
그럼 이제 또 다른 문제에 직면합니다. 어떻게 이 MSE를 줄여나갈 수 있을까?
우리는 손실함수를 최소화하는 방향으로 파라미터를 업데이트 하기 위해 Gradient Descent(경사하강법)이라는 알고리즘을 사용합니다. 이 알고리즘은 한마디로 cost를 최소하 하는 방향으로 동작을 하는 알고리즘인데요.
이때 미분을 사용하게 됩니다.
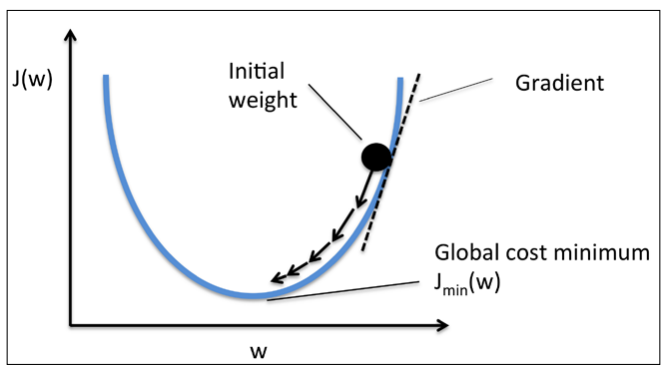
이해를 단순하게 하기 위해 w에 대해서만 생각해봅시다.
만약 데이터가 x = [1,2,3] y = [1,2,3] 이라 하면, w = 0 일때 y(hat) = [0,0,0]으로 cost[w] = MSE = 4.67, w = 1일때 cost[w] = 0
w = 2일때 y(hat) = [2,4,9], cost[w] = MSE = 4.67로, x 축을 w, y축을 cost라 했을 때, 그래프를 그려보면 w = 1을 기점으로
2차원 그래프가 그려지게 됩니다. 이때 경사하강법은 현재 스텝의 파라미터에서 비용함수의 미분값에 learning rate라 하는 α 값을 곱한만큼을 빼서 다음스텝의 파라미터값으로 지정합니다. 공식으로 표현하면 아래와 같은데요. 전혀 어려운 공식이 아닙니다!

여기서 러닝레이트란, 한 번에 얼마나 업데이트할지 정해주는 파라미터입니다. 만약 러닝레이트가 크면 빠르게 학습할 수 있어 학습 시간을 단축 할 수 있지만, 그 변화폭이 크기 때문에 (한번에 w 값이 크게 변하기 때문에), 최적의 w값을 건너 뛸 수 도 있게 됩니다. 즉 최적의 값을 찾지 못하고 발산해 버리는것이죠. 그렇기 때문에 적절한 런닝레이트를 설정해야 합니다. (정답은 없습니다만, 보통은 0.01로 두고 한다고? 합니다.)
다시 공식으로 돌아와서 공식을 살펴보면, 초기의 w가 어디서 시작하던, 업데이트 할 수록 w에 가까워 지게 됩니다. cost가 제일 낮은 지점에 가까워 질 수록, 비용함수의 미분값도 0에 수렴하기 때문에 정답 w에 가까워지게되면 빼거나 더하는 값도 0에 수렴하게 되죠. (하지만, 단순 2차원그래프의 경우 저점이 하나이기 때문에 문제가 없지만, 2차원 그래프가 아닌 고차원 그래프의 경우, 저러한 local minimum이 여러개 있는데, 하나의 저점에 같혀버려 더 낮은 저점(global minimum)을 찾지 못하게 되는 문제가 발생 할 수 있다고? 합니다.)
아무튼! 이러한 원리로 각각의 파라미터들을 업데이트 하게 되는거랍니다. 그렇게 어려운 개념이 아님에도 우와! 하게 되지 않나요? ㅎㅎ
비용함수의 원리에대해서도 알게되었고! 경사하강법이 어떤식으로 동작하는지도 알게 되었으니! 실제로 코드로 구동시켜 봅시다! 실제로 학습이 잘 되서 결과를 잘 도출 하는지 확인 해봐야죠@@
import tensorflow.compat.v1 as tf
tf.disable_v2_behavior()
x_train = [1,2,3] # x데이터
y_train = [1,2,3] # y데이터 (레이블)
w = tf.Variable(tf.random_normal([1]), name = 'weight') # weight 과 bias 초기값 랜덤하게 설정
b = tf.Variable(tf.random_normal([1]), name = 'bias')
hypothesis = x_train*w + b # 가설!
cost = tf.reduce_mean(tf.square(hypothesis - y_train)) # 비용(손실) 함수 정의!
# square = 제곱, reduce_mean = 평균을 내고 차원을 한 차원 내립니다.
# ex) t = [1.,2.,3.,4.], tf.reduce_mean(t) = 2.5
#런닝레이트 0.01, 그레디언트 디센트 !
optimizer = tf.train.GradientDescentOptimizer(learning_rate = 0.01)
train = optimizer.minimize(cost) # 비용 최소화
sess = tf.Session() #세션 만들기
# 변수 초기화!(중요), 세션을 열고나서 꼭 변수를 초기화 해줘야 합니다.
sess.run(tf.global_variables_initializer())
for step in range(2001):
sess.run(train)
if step % 20 == 0:
# 20번 마다 비용, w, b 값 출력
print(step, sess.run(cost), sess.run(w), sess.run(b))
sess.close() # 세션 닫기
프로그램을 실행한 후 결과를 분석해 볼까요?

x와 y가 각각 [1,2,3], [1,2,3] 이기 때문에 우리는 y = x라는 식에 가까워져야 합니다.
처음에는 비용함수가 4.2로 생각보다 큰것을 볼 수 있습니다. w 와 b도 각각 0.6, -1.2 로 y = 0.6x -1.2 가 되겠네요. 하지만 20번째를 보니 급격히 비용함수가 낮아진것을 볼 수 있습니다. w와 b도 정답에 가까워 졌고요

2000번째 결과를 보면 ! 비용함수가 엄청 낮아지고, w는 1에 수렴 b는 0에 수렴한것을 볼 수 있습니다.
즉 y = x랑 99.999..% 일치하는 거죠. 신기하지 않나요? 앞전에 placeholder를 배워봤으니 이번에는 placeholder를 사용해 봅시다!
import tensorflow.compat.v1 as tf
tf.disable_v2_behavior()
w = tf.Variable(tf.random_normal([1]), name = 'weight')
b = tf.Variable(tf.random_normal([1]), name = 'bias')
x = tf.placeholder(tf.float32)
y = tf.placeholder(tf.float32)
hypothesis = w*x +b
cost = tf.reduce_mean(tf.square(hypothesis - y))
optimizer = tf.train.GradientDescentOptimizer(learning_rate = 0.01)
train = optimizer.minimize(cost)
sess = tf.Session()
sess.run(tf.global_variables_initializer())
for step in range(2001):
cost_val, w_val, b_val, _ = sess.run([cost, w, b, train], feed_dict={x: [1, 2, 3, 4, 5], y: [2.1, 3.1, 4.1, 5.1, 6.1]})
if step%20 ==0:
print(step,cost_val,w_val,b_val)placeholder를 사용함으로써 x데이터와 y데이터에대해 가변하게 줄 수 있게 되었습니다. 이번에는
x = [1,2,3,4,5] ,y = [2.1, 3.1, 4.1, 5.1, 6.1] 데이터를 갖고 학습을 하는데, 만약 제대로 동작 한다면,
y = x + 1.1 이 나와야 합니다. 즉 w = 1 b = 1.1 이 나와야죠. 결과를 한 번 볼까요?
역시 처음에는 비용함수가 크게 나오고 w와 b 값이 잘 들어맞지 않지만, 횟수를 거듭하며
점점 비용함수가 내려가는것을 볼 수 있습니다 ㅎㅎ


비용함수가 점점 내려가면서, 결국 w = 1, b = 1.1에 가깝게 결과가 도출 되었네요!
2021.02 TensorFlow 2.x 버전 추가)
import tensorflow as tf
x_data = [1, 2, 3] # x데이터
y_data = [1, 2, 3] # y데이터 (레이블)
# w, b 초기화
w = tf.Variable(5.8)
b = tf.Variable(1.0)
# 러닝레이트
learning_rate = 0.01
for i in range(2001):
# GradientTape을 사용해 경사도 계산
with tf.GradientTape() as tape:
hypothesis = w * x_data + b
cost = tf.reduce_mean(tf.square(hypothesis - y_data)) # MSE
w_grad, b_grad = tape.gradient(cost, [w, b]) # gradient 업데이트
w.assign_sub(learning_rate * w_grad) # W 갱신, assign_sub: A.assing_sub(B)는 A -= B와 같음
b.assign_sub(learning_rate * b_grad) # b 갱신
if i % 100 == 0:
print("{:5}|{:10.4f}|{:10.4}|{:10.6f}".format(i, w.numpy(), b.numpy(), cost))
너무 재밌지 않나요? 다음에 더 재밌는 내용으로 찾아 오겠습니다 ㅎㅎ 읽느라 수고 많으셨습니다!
'머신러닝' 카테고리의 다른 글
| Logistic regression(로지스틱 회귀!) (0) | 2020.02.19 |
|---|---|
| Multi-variable linear regression(다중선형회귀) (0) | 2020.02.07 |
| 입문자 초보자를 위한 텐서플로 기초 API (0) | 2020.02.06 |
| 머신러닝 입문자, 초보자를 위한 내용 정리 (+Tensorflow) (0) | 2020.02.05 |
| TensorFlow 2.0 에서 TensorFlow 1.0 , 1.x 버전 코드 실행하기 (0) | 2020.02.05 |
