티스토리 뷰
앞서 머신러닝에 대해 배웠다면, 이제 본격적으로 딥러닝에 대해 공부해 볼 시간입니다!
딥러닝 하면 많이 들어봤을 CNN RNN을 공부하기에 앞서, ANN, 즉 인공신경망이 뭔지 짚고 넘어가려 합니다.
ANN은 Artificial Neural Network의 약자로, 인공신경망을 의미합니다. 인공신경망은 그 이름에서 알 수 있듯이, 뇌에서 영감을 받은 학습 알고리즘 입니다. 각각의 뉴런이 다음 뉴런으로 다양한 세기의 신호를 보내면서 문제를 해결하는 시스템을 모방한 것이죠.
하나의 뉴런이 다양한 뉴런으로부터 신호를 받고 다음 뉴런으로 신호를 보내듯이, ANN역시 똑같은 매커니즘을 거칩니다. 다양한 input data를 받아 각각의 가중치가 곱해지고 bias가 더해져 다음 노드로 전달되는것이죠.
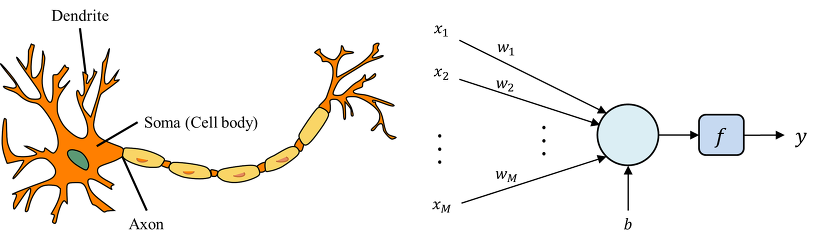
이런 뉴런을 공학적인 구조로 변형한것이 바로 퍼셉트론입니다. 좌측이 뉴런이고 우측이 퍼셉트론이라 할 수 있죠. 퍼셉트론은 입력층과 출력층을 갖으며, 인풋 데이터 x에 가중치 w를 곱하고 바이어스를 더한값을 활성 함수(activation function)의 입력값으로 받아 0또는 1의 값을 출력합니다.

계속 이어나가기 전에, 옛날에 머신러닝 분야에서 해결하지 못하던 문제가 있었는데요. 그 문제가 바로 XOR문제 입니다. 앞서 배웠던 머신러닝 기법으로 and 나 or같은 문제는 잘 학습시켜 문제를 해결 할 수 있었지만, xor의 경우 학습을 통해 문제해결하기가 무척 어려웠습니다. 그림을 보시면 왜 어려운지 이해할 수 있는데요.
비전공자분들을 위해 간단히 설명 드리자면, and와 or xor는 각각의 연산을 했을 때 다음과 같은 결과가 나오게 됩니다.
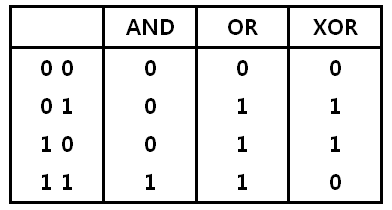

그래프에 나타내면 위와 같이 나타낼 수 있습니다. AND와 OR의 경우 단순히 linear하게 선을 그어 각각의 경우를 나눌 수 가 있는데요. XOR의 경우 선을 어떻게 그어도 구분지을 수가 없습니다.
이를 해결하기 위해 나온 개념이 바로 퍼셉트론을 여러층 쌓아 올린 다층퍼셉트론(Multi Layer Perceptron) 구조 입니다. 이 MLP는 입력층(Input layer) - 은닉층(Hidden layer) - 출력층(Output layer)으로 구성되어 있습니다.
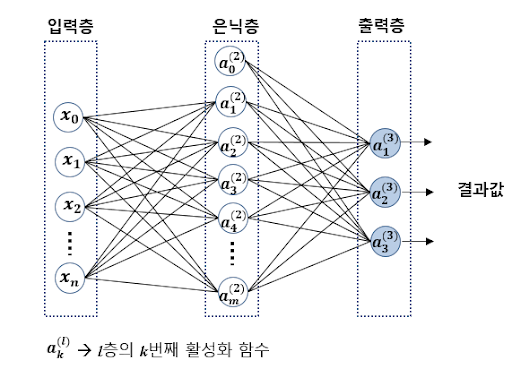
하나의 퍼셉트론은 단순히 0과 1 이진분류만 가능하지만, 다층퍼셉트론 구조에서는 비선형적인 특징을 학습할 수 있습니다. 활성함수로는 시그모이드 함수와 쌍곡 탄젠트 그리고 ReLU가 사용될 수 있는데, ReLU를 가장 많이 사용합니다.
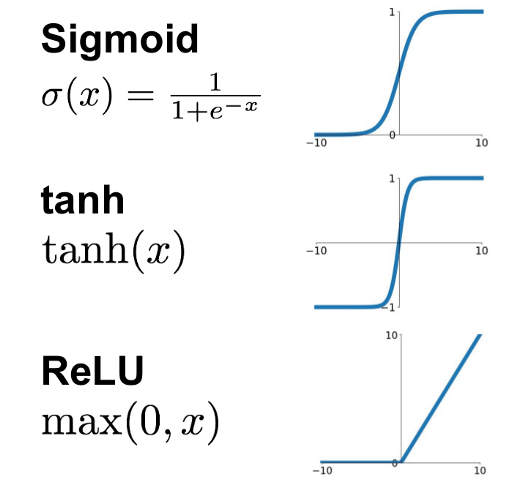
sigmoid와 tanh함수는 입력값 x가 너무 커지거나 작아지면 그래프의 미분값(기울기)이 0이되는 문제가 발생 합니다. 하지만, ReLU의 경우 입력값 x가 0보다 작으면 미분값이 0이지만, 0보다 클 경우 입력값이 아무리 커져도 미분값이 1인 상태가 유지되기 때문에 Vanishing Gradient Problem이 발생할 확률이 더 적습니다.
Vanishing Gradient Problem이 뭔지 알고싶다면 ? - https://brunch.co.kr/@chris-song/39
ReLu는 뒤에서 살펴보기로 하고, 활성함수로 sigmoid를 사용하여, 단순한 뉴럴넷을 만들어보면, 이제 XOR문제를 풀 수 있습니다!

단지 세개의 퍼셉트론을 연결 함으로써 해결이 가능한데요. 직접 해보시면 다음과 같이 나오는 것을 볼 수 있습니다. (직접 해보시걸 추천합니다!. 잘 이해가 안가신다면, 모두의 딥러닝 시즌 1 해당 부분을 참고하세요 :) )

하지만, 이렇게 결과가 잘 나올 수 있는 이유는 우리가 가중치 w와 바이어스 b를 잘 설정해주었기 때문인데요. 그럼 이런 뉴럴넷, MLP 의경우 학습은 어떻게 시킬까요?
오류 역전파 알고리즘 (Backpropagation Algorithm)
MLP역시 다른 머신러닝 알고리즘과 마찬가지로 경사하강법을 이용해 파라미터를 업데이트 하면서 학습합니다. 경사하강법을 수행하려면, 손실함수(비용함수)의 미분값을 계산해야 하는데 MLP의 경우 여러개의 노드와 층으로 구성되어 있어 각각의 노드에서 미분값을 계산하는것이 쉽지 않았습니다. 각각의 노드의 미분값이 다른 노드의 미분값에 영향을 주기 때문이죠. 그래서 도입된 것이 바로 미분에서의 체인 룰(Chain Rule) 입니다.

오류 역전파란, 이름 그대로 오류를 뒤에서 앞으로(출력에서 입력층으로) 전달하며 파라미터를 업데이트 하는 것 입니다.
오류를 뒤에서 앞으로 전달 하는 것은 결국 신경망 전체 구조를 합성함수로 간주하고 , 각각의 노드들을 합성함수를 구성하는 각각의 함수로 간주하여 체인룰을 푸는것으로 해석가능 합니다.
즉 다음의 과정을 통해 학습이 진행 됩니다.
- 트레이닝 데이터를 입력층에 넣어 전방향연산(Forward-propagate) 수행, 결과로 나온 MLP 예측 값과 실제 답과의 차이인 에러를 계산
- 에러를 MLP의 각 노드들에 역전파(Back propagate)

그럼 간단한 예시를 통해 내용을 더 잘 이해해봅시다!
참고로 아래의 예시는 모두의 딥러닝 시즌 1의 내용입니다.

인풋 x에 가중치 w를 곱하고 바이어스 b를 더한 f = wx+b는 위와 같이 f = g+b로 나타낼 수 있고, (g = wx)
각각 w, x b가 f에 영향을 끼치는 정도를 미분으로 나타내면 위와 같이 나타낼 수 있습니다.

w = -2, x = 5, b= 3일 때 오류 역전파법을 통해 f를 각각 w와 x, b로 편미분 하면, 그 미분 값으로 5, 2 ,1 이 나오게 되는데 이 숫자는 출력에 얼마나 영향을 끼치는지 척도가 됩니다. f를 w로 편미분한 값이 5로 가장 큰것을 알 수 있는데, 실제로 계산해보면 w가 조금만 변해도 f값이 크게 달라지는 것을 알 수 있습니다.
실제로 w와 x, b를 각각 1씩 뺀 w = -1 , x =4, b =2라 했을 때 즉,
case1. (w = -1, x= 5, b= 3) case2. (w = -2, x= 4, b= 3) case3. (w = -2, x= 5, b= 2) 를 비교해보면
case1. f = -2 (원래 값과 차이 5) case2. f = -5 (원래 값과 차이 2) case3. f = -8 (원래 값과 차이 1)
w의 값의 변화가 f의 결과에 가장 큰 영향을 끼치는 것을 볼 수 있습니다.
다음 포스팅에서는 뉴럴넷을 이용해 코드로 XOR문제를 풀어보겠습니다 :)
'머신러닝' 카테고리의 다른 글
| TensorFlow, No module named 'tensorflow.examples.tutorials' 문제 해결 방법 (0) | 2020.03.17 |
|---|---|
| Neural Network 실습, XOR 문제풀기 & MNIST 숫자 분류기 (0) | 2020.03.17 |
| learning rate & overfitting & 학습 데이터.. (2) (0) | 2020.02.25 |
| learning rate & overfitting & 학습 데이터.. (1) (0) | 2020.02.24 |
| Softmax & cross entropy (1) | 2020.02.24 |
