티스토리 뷰
보통 코딩 테스트를 볼 때, 조금 난이도가 있는 문제는 알고리즘의 정확성 테스트뿐만이 아니라 효율성 테스트를 함께 검토하게 됩니다.
즉 알고리즘을 잘 구현해서 정답을 잘 맞춰도 효율이 좋지 못하면.. 효율성 테스트를 통과하지 못하게 되는데요.
이럴 경우, 정확성 부분에만 부분점수를 받을수도, 아예 점수를 받지 못할 수도 있습니다.
이 효율성테스트라는 것이 시간 복잡도를 의미합니다. 결국 이 알고리즘이 얼마나 문제를 빨리 풀어낼 수 있는지 체크하는 것이라 할 수 있습니다.
저 같은경우, 딱 문제를 보고 직관적으로 생각나는 방법으로 풀면 무조건 시간 복잡도가 O(n^2)이 나오더라구여 ㅜㅜㅜ
보통 효율성 테스트를 통과하기 위해서는 시간복잡도가 O(nlogn)이 되어야 하는 것 같습니다.
알고리즘을 처음 공부하시는 분들은 O(n^2) ?? O(nlogn)?? 무슨 말을 하는 거지? 하실 것 같은데요. 오늘 설명 드릴 부분이 바로 이 빅오 표기법에 대한 부분입니다.
어떤 문제를 보고 알고리즘을 짤 때, 그 문제의 해결방법은 정말 다양하게 나 올 수 있습니다. (실제로 알고리즘 연습 사이트에서 문제를 풀고 나서 다른 사람의 풀이를 보게 되면, 정말 다양한 풀이 방법이 있구나! 하는 걸 느끼게 됩니다.)
해결방법이 다양한 만큼 그 각각의 방법들이 문제를 해결하는데 소요되는 시간도 다 다를 수 있습니다.
이 처럼, 시간복잡도란 알고리즘이 문제를 해결하는데 걸리는 시간과 입력의 함수 관계를 나타내며, 이를 표현하는 방식이 바로 빅오 표기법입니다.
참고로 공간복잡도라는 개념도 있는데, 공간 복잡도는 해당 알고리즘이 얼마만큼의 메모리를 사용하는지를 나타내는 지표라 보시면 될 것 같습니다. 하지만, 과거와는 다르게 컴퓨터 성능이 급격히 발달함으로써, 현재는 공간 복잡도의 중요도가 많이 낮아진 것 같습니다. (아 그렇다고 중요하지 않다는 건 아닙니다!)
빅오 표기법(Big-O notation)은 점근적 묘사 방법으로 다음과 같이 표현 할 수 있습니다. 대문자 O에 괄호를 하고 안에 계수를 뺀 차수가 가장 큰 항을 넣어주면 됩니다.

만약 시간복잡도를 나타내는 어떤 함수가 3n^2+5n+42 라면, 빅오 표기법으로 나타낼 경우 계수는 제외하고 가장 큰 차수만 고려하기 때문에 O(n^2)이 됩니다. 왜 그럼 가장 큰 차수만 고려할까요? 빅오 표기법에 대한 수학 정의가 있지만, 간단하게 말하면, 자료의 개수가 많은 경우에는 차수가 가장 큰 항이 가장 영향을 크게 미치기 때문에 다른 항들은 상대적으로 무시될 수 있습니다. 실제로, n^2과 n만 비교해 봐도, 100을 넣었을 때 각각 10000과 100으로 n이 시간 복잡도에 끼치는 영향이 상당히 미비한 것을 알 수 있죠.
알고리즘에서 자주 접하는 시간복잡도는 다음과 같습니다.
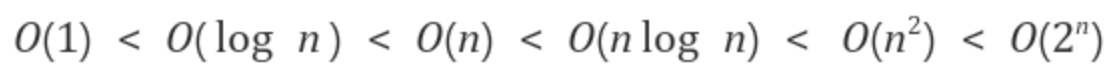
우측으로 갈 수록 시간 복잡도의 효율성이 좋지 못합니다. 이를 그래프로 확인하면, 더 잘 체감할 수 있는데, 보이시나요???
자료의 개수(x축)가 150까지밖에 안되지만, 그래프의 기울기가 급격히 변하는 것을 볼 수 있습니다.
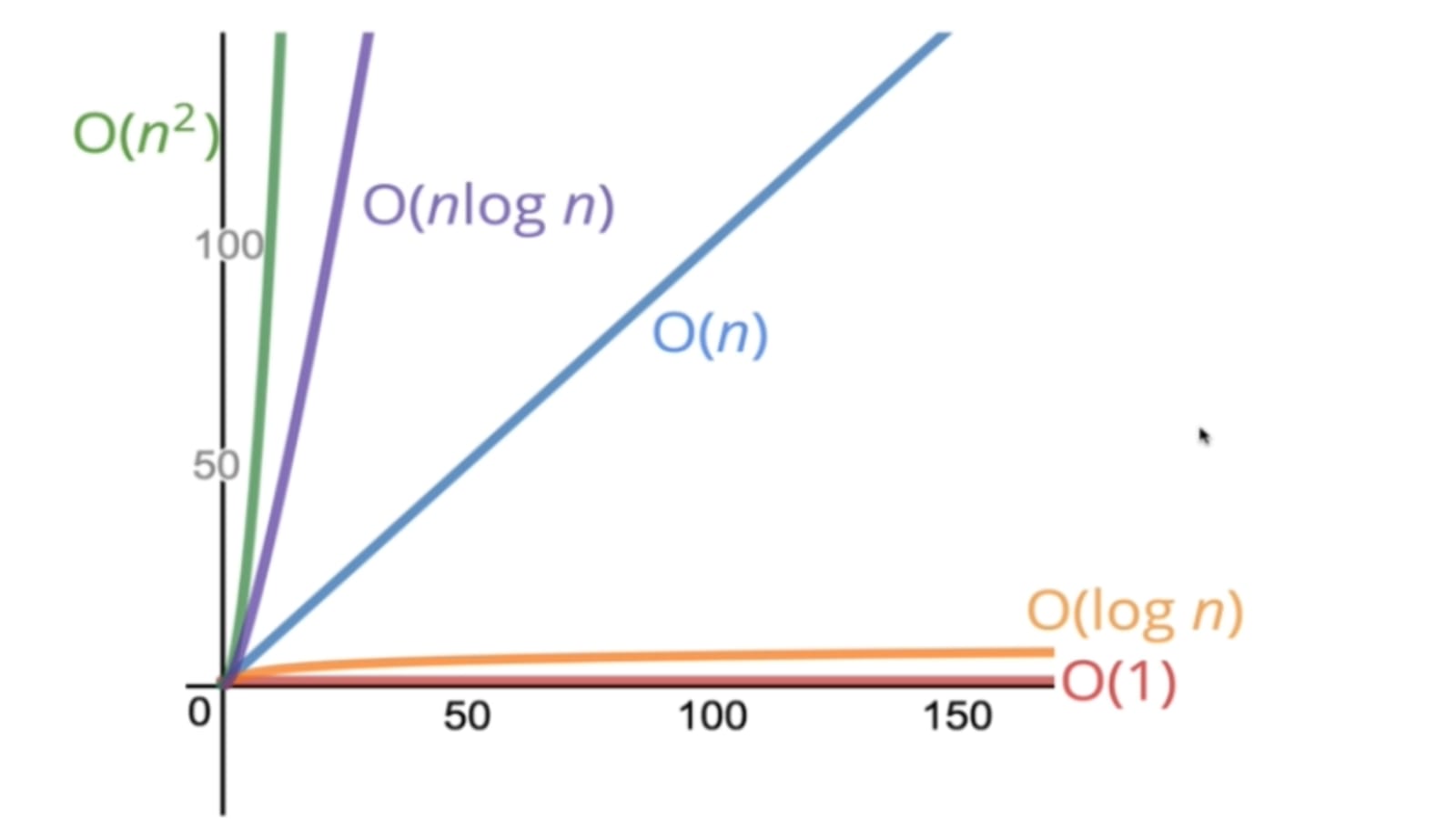
다음은 대표적인 빅오 표기법의 예입니다.

저는 보통 반복문을 중첩해버리는 바람에 효율성을 통과하지 못하는경우가 많았습니다. ㅜㅜ
보통 직관적으로 떠오르는 방법이면서 쉬운방법이 반복문의 중첩이라.. ㅎㅎ 하지만, 이렇게 하면 절대 절대 절대 효율성 테스트는 통과 못합니다. 그래서, 단순히 정확성만 평가하는 문제 말고 효율성도 함께 평가하는 문제들을 많이 풀어보는 게 좋을 것 같습니다.
읽어주셔서 감사합니다!
'알고리즘 > 정리' 카테고리의 다른 글
| 정규표현식(regex) 알아 보기, 어렵지 않아요! (2) | 2021.03.23 |
|---|---|
| 기본 정렬 알고리즘 알아보기 with Python (0) | 2020.09.29 |
| 알고리즘 순서도 그리는 방법, 알고리즘 공부 법 (1) | 2020.05.26 |
