티스토리 뷰
오늘은 기초적인 정렬 알고리즘을 알아보려 합니다.
대표적인 정렬 알고리즘으로는 선택 정렬, 버블 정렬(거품 정렬), 삽입 정렬, 셸 정렬(쉘 정렬), 병합 정렬, 퀵 정렬 등이 있는데요.
간단하게 선택 정렬, 버블 정렬, 삽입 정렬, 쉘 정렬 네 가지 정렬의 정의와 코드를 정리하고 각각의 알고리즘 실행 속도를 측정하여 성능을 비교해 보려 합니다.
1. 선택 정렬
주어진 배열에서 가장 작은 원소를 찾아 첫 번째 원소와 교환하고 두 번째 작은 원소를 찾아 두 번째 원소와 교환하고... 반복하는 정렬 방법
정렬 방법
1. 주어진 배열 중 최솟값을 찾는다.
2. 그 최솟값을 맨 앞의 원소와 교환한다.
3. (N-1)원소에 대해 1-2 방법 반복
소스코드(파이썬)
def select_sort(a: list) -> list:
n = len(a)
for i in range(0, n-1):
min_idx = i
for j in range(i + 1, n):
if a[j] < a[min_idx]:
min_idx = j
a[i], a[min_idx] = a[min_idx], a[i]
return a특징: 제자리 정렬 알고리즘 (정렬에 사용되는 추가적인 저장공간이 매우 작음), 불안정적인 정렬 (같은 값일 때 순서가 변할 수 있음)
시간 복잡도: O(N^2)
2. 버블 정렬
두 인접한 원소를 비교하여 정렬하는 방법, 루프를 한번 반복할 때마다 가장 큰 값이 맨 뒤로 이동
정렬 방법:
1. 인접한 두 수 비교 및 교환
2. (배열 원소의 개수 - 루프 반복 횟수) 만큼 1번 과정 반복
소스코드(파이썬)
def bubble_sort(a: list) -> list:
n = len(a)
for i in range(n-1):
for j in range(n-i-1):
if a[j] > a[j+1]:
a[j], a[j+1] = a[j+1], a[j]
return a특징: 제자리 정렬 알고리즘 (정렬에 사용되는 추가적인 저장공간이 매우 작음), 안정적인 정렬 (같은 값이어도 정렬 후 순서가 변하지 않음)
시간 복잡도: O(N^2)
3. 삽입 정렬
자신이 삽입될 위치를 찾아 자리를 만들고 그 위치에 삽입하여 정렬하는 방법
정렬 방법:
1. 배열의 원소를 앞에서부터 차례대로 이미 정렬된 배열과 비교(삽입될 위치 찾기)
2. 삽입될 위치에 원소 삽입
3. 정렬 완료까지 1-2 과정 반복
소스코드(파이썬)
def insert_sort(a: list) -> list:
n = len(a)
for i in range(1, n):
key = a[i]
j = i - 1
while j >= 0 and a[j] > key:
a[j+1] = a[j]
j-= 1
a[j+1] = key
return a특징: 제자리 정렬 알고리즘 (정렬에 사용되는 추가적인 저장공간이 매우 작음), 삽입할 때마다 배열의 원소를 이동시켜야 하므로 배열 크기가 큰 경우 비효율적, 안정적인 정렬 (같은 값이어도 정렬 후 순서가 변하지 않음)
시간 복잡도: O(N^2)
4. 셸 정렬
삽입 정렬을 보완한 형태의 정렬 방법으로 삽입 정렬이 초기 리스트가 거의 정렬되어있을 때 효율적이라는 점에서 착안한 정렬 방법, 멀리 떨어져 있는 원소들을 미리 교환시켜 정렬 속도를 향상시킨 방법
정렬 방법:
1. 간격 h 설정 (보통은 정렬할 배열의 길이 / 2) [but, h = 3*(n-1)+1로 설정할 때 가장 좋은 성능을 낸다고 알려져 있습니다.] ex) h = 1,4,13,40,121.....
2. 첫 번째 원소와 첫 번째 원소로부터 h 배수만큼 간격이 있는 원소들에 대한 부분 배열 삽입 정렬 수행
3. 간격 h를 줄여나가며 삽입 정렬 반복
소스코드(파이썬)
def shell_sort(a: list) -> list:
h = 1
n = len(a)
while h < n:
h = 3*h + 1
h = h//3
while h > 0:
for i in range(h,n):
k=i-h
key=a[i]
while k>=0 and key < a[k]:
a[k+h] = a[k]
k=k-h
a[k+h] = key
h = h//3
return a특징: 제자리 정렬 알고리즘 (정렬에 사용되는 추가적인 저장공간이 매우 작음), 불안정적인 정렬 (같은 값일 때 순서가 변할 수 있음)
시간 복잡도: O(N(logN))~O(N^4/3)
이제 각각의 정렬 알고리즘들의 실행 시간을 측정해보겠습니다.
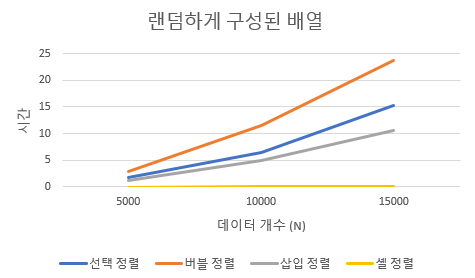
case1. 랜덤 하게 구성된 배열
| 데이터 개수(N) | 선택 정렬 | 버블 정렬 | 삽입 정렬 | 셸 정렬 |
| 5000 | 1.71 | 2.89 | 1.22 | 0.03 |
| 10000 | 6.42 | 11.51 | 4.98 | 0.057 |
| 15000 | 15.26 | 23.7 | 10.65 | 0.092 |
case2. 정렬된 배열
| 데이터 개수(N) | 선택 정렬 | 버블 정렬 | 삽입 정렬 | 셸 정렬 |
| 5000 | 1.28 | 1.73 | 0.0013 | 0.0097 |
| 10000 | 4.85 | 6.27 | 0.0029 | 0.021 |
| 15000 | 10.49 | 14.38 | 0.0046 | 0.042 |

case3. 역순으로 정렬된 배열
| 데이터 개수(N) | 선택 정렬 | 버블 정렬 | 삽입 정렬 | 셸 정렬 |
| 5000 | 2.15 | 3.98 | 2.57 | 0.016 |
| 10000 | 11.64 | 14.81 | 9.29 | 0.038 |
| 15000 | 19.63 | 33.53 | 24.69 | 0.044 |
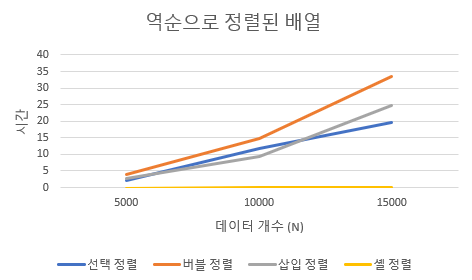
보시면 아시겠지만 모든 경우에 대해서 전반적으로 셸 정렬이 가장 빠른 것을 볼 수 있으며 버블 정렬이 가장 느린 것을 볼 수 있습니다 ㅎㅎ
또 삽입 정렬과 버블 정렬의 경우 정렬된 순서에 민감하게 반응하는 것을 볼 수 있는데요. 아무래도 버블 정렬은 정렬 과정에서 계속 교환을 하고 삽입 정렬 역시 정렬 과정에서 계속 레코드를 이동시켜야 하기 때문으로 생각됩니다.
다음 포스팅에서는 퀵 정렬, 합병 정렬, 힙 정렬에 대해 알아보겠습니다.
읽어주셔서 감사합니다 :)
'알고리즘 > 정리' 카테고리의 다른 글
| 정규표현식(regex) 알아 보기, 어렵지 않아요! (2) | 2021.03.23 |
|---|---|
| 알고리즘 시간 복잡도와 빅오 표기법 (0) | 2020.05.28 |
| 알고리즘 순서도 그리는 방법, 알고리즘 공부 법 (1) | 2020.05.26 |
