티스토리 뷰
탐색 알고리즘? - 컴퓨터에 저장된 자료를 신속하고 정확하게 찾아주는 알고리즘
이진 탐색(binary search)
정렬되어 있는 배열에서 특정한 값을 찾아내는 알고리즘으로 탐색 시간 복잡도는 O(logN)
탐색 방법: 분할-정복 방법 사용
ex) 정렬된 배열 [12,15,23,48,62,98,111,130] 에서 23을 찾는다면??
1. 가운데 값 선택 -> 48
2. 우리가 찾고자하는 23은 48 좌측에 위치함으로 탐색범위가 12~23으로 줄어듬, 줄어든 탐색범위에서 중간 값 선택 -> 15
3. 23은 15 우측에 위치, 값은 하나만 남게 되고 이 값은 23과 일치
소스코드(파이썬)
def binary_search(a:list, search_key):
left, right = 0, len(a)
while left<=right:
mid = (left + right) // 2
if a[mid] == search_key: return mid
if a[mid] > search_key: right = mid - 1
else: left = mid+1
return -1
이진 탐색 트리(binary search tree)
이진 탐색 트리
작은키를 갖고 있는 모든 레코드는 왼쪽 부분 트리에 있음
같거나 큰 키를 가지고 있는 모든 레코드는 오른쪽 부분 트리에 있음
각각의 부분트리 역시 이진 탐색 트리임
ex) [27, 14, 35, 10, 19, 31, 42]
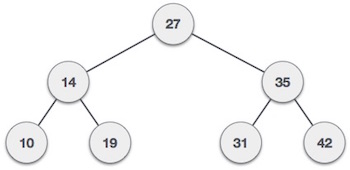
핵심 연산 - 1. 삽입 2. 삭제 3. 탐색
삽입: item삽입의 경우 입새 노드(leaf node)에 추가
삭제: item 삭제 시, 이진 탐색 트리 조건을 유지하기 위해 적절한 조치 필요
www.cs.usfca.edu/~galles/visualization/BST.html 이 링크를 통해 삽입 삭제 탐색 연산을 시뮬레이션 해볼 수 있습니다!
탐색 방법:
1. 루트와 주어진 키 비교
2. 키가 루트보다 작다면, 왼쪽 부분트리로 이동, 키가 루트보다 크다면 오른쪽 부분트리로 이동
3. 키가 루트와 같다면 종료 (1-2 과정 재귀적인 방법으로 구현)
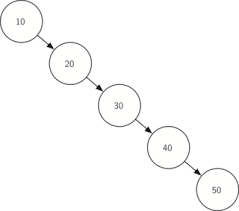
탐색 시간복잡도: 평균 - O(logN), 최악 - O(N) -> 트리의 균형이 한쪽으로 쏠려 있는 경우 탐색 시간이 늘어남 ex) 키가 정렬되어 있는 경우 모든 item이 한쪽으로 쏠려 시간 복잡도가 O(N)이 됨
소스코드(파이썬)
# 이진 탐색 트리
class Node:
def __init__(self, data):
self.data = data
self.left = self.right = None
class BinarySearchTree:
def __init__(self):
self.root = None
def insert(self, data):
self.root = self.insert_value(self.root, data)
return
def insert_value(self, node, data):
if node is None:
node = Node(data)
else:
if data <= node.data:
node.left = self.insert_value(node.left,data)
else:
node.right = self.insert_value(node.right,data)
return node
def find(self,search_key):
return self.find_value(self.root, search_key)
def find_value(self, root, search_key):
if root is None or root.data == search_key:
return root is not None
elif search_key > root.data:
return self.find_value(root.right, search_key)
else:
return self.find_value(root.left, search_key)
bst = BinarySearchTree()
arr = [27, 14, 35, 10, 19, 31, 42]
for x in arr:
bst.insert(x)
print(bst.find(19)) # 19 존재O 결과: True
print(bst.find(30)) # 30 존재x 결과: False
# 중위 순회
def inorderTraversal(node):
if not node.left == None : inorderTraversal(node.left)
print(node.data, end='\n')
if not node.right == None : inorderTraversal(node.right)
inorderTraversal(bst.root) *트리를 중위순회하면 정렬된 상태로 출력 가능
'알고리즘' 카테고리의 다른 글
| [알고리즘] Dynamic programming (동적 계획법) 완전정복 with Python (4) | 2020.12.31 |
|---|---|
| [알고리즘] 탐색(3) - AVL 트리 (0) | 2020.12.06 |
| [알고리즘] 탐색(2) - 레드 블랙 트리 파이썬 구현 (1) | 2020.12.05 |
| [알고리즘] 탐색(2) - 레드 블랙 트리 (0) | 2020.12.05 |
| 시간복잡도 O(NlogN)정렬 알고리즘 알아보기 with Python (0) | 2020.11.28 |
