티스토리 뷰
AVL트리 역시 레드-블랙 트리와 마찬가지로 자가 균형 이진 탐색 트리입니다.
레드-블랙 트리와 다른 점은 균형(balance)을 유지하기 위해 적용하는 조건이 다른데요. 그래서 같은 자가 균형 이진 탐색 트리이지만 같은 키를 삽입해도 트리의 결과는 다르게 나올 수 있습니다.
ex) KEY = [2, 1, 8, 9, 7, 3, 6, 4, 5] 삽입 시
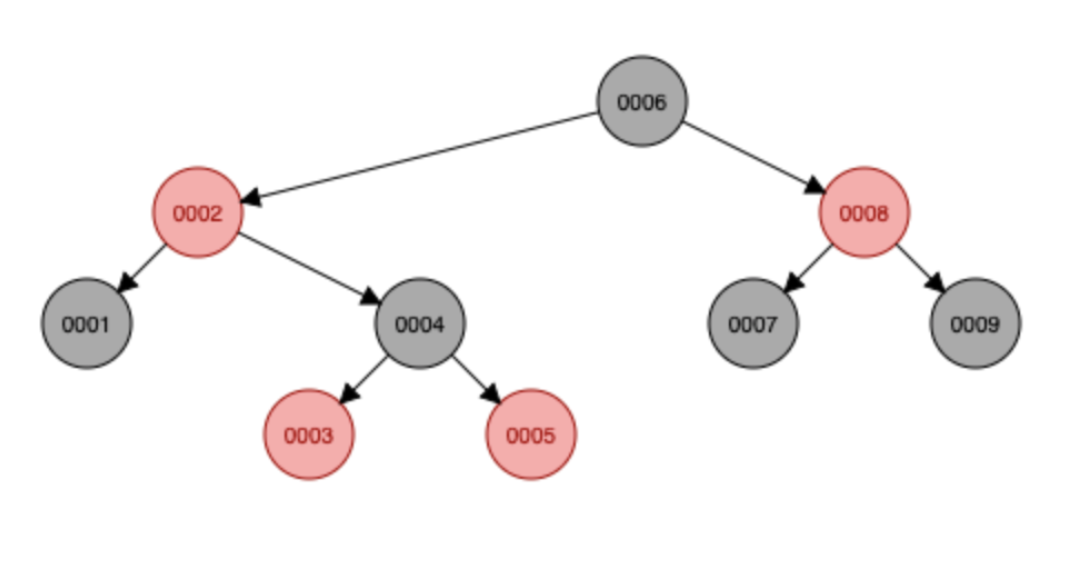

AVL트리 조건은 다음과 같습니다.
1. *높이 차가 2 이상이 되면 회전을 통해 높이차를 1 이하로 유지
* 높이 차 = 오른쪽 서브 트리의 높이 - 왼쪽 서브 트리의 높이
조건은 엄청 간단하죠??
여기서 높이 차에 대해 예시를 통해 설명드리자면
각각의 노드 옆에 높이차를 적게 되는데, 이 높이 차는 해당 노드의 우측 서브 트리 높이- 왼쪽 서브 트리 높이입니다.

이제 이 높이차가 2 이상이 되면 회전을 통해 높이차를 1 이하로 유지시켜 줘야 하는데
이 회전에는 LL 회전, RR 회전, LR회전, RL회전 총 4가지가 있습니다.
종류가 많아 보일 수도 있지만 엄청 간단하니 겁먹지 않으셔도 됩니다 ㅎㅎ
1. LL 회전 (트리가 왼쪽으로 치우쳐 있는 경우)
Step 1. 가운데 노드를 부모 노드로 나머지 두 노드를 자식 노드로 변환
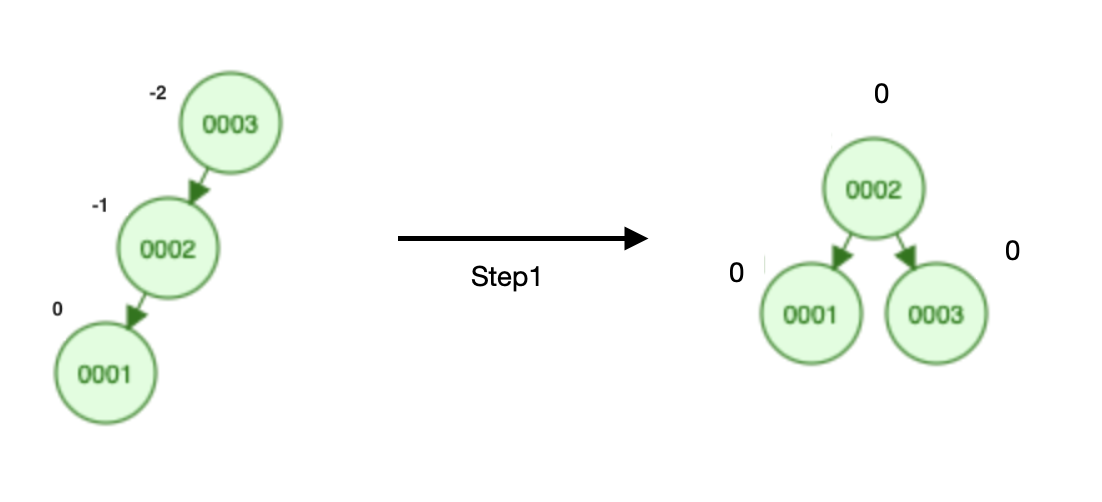
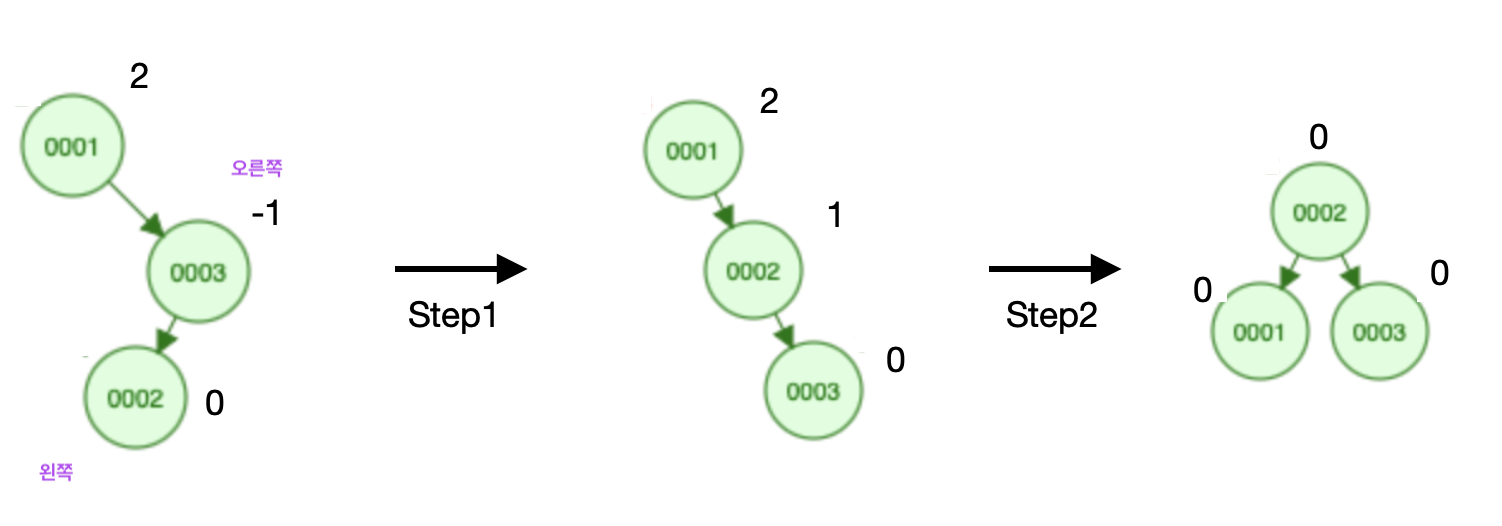
2. RR 회전 (트리가 오른쪽으로 치우쳐 있는 경우)
Step 1. 가운데 노드를 부모 노드로 나머지 두 노드를 자식 노드로 변환

3. LR 회전 (트리가 왼쪽 -> 오른쪽으로 치우쳐 있는 경우)
Step 1. 맨 하단의 노드(가장 작은 key값을 가진 노드)를 가운데로 이동
Step 2. 가운데 노드를 부모 노드로 나머지 두 노드를 자식 노드로 변환
(step 1, step 2 를 묶어서 생각하면 결국 세 개의 키 값 중 가운데 값을 부모 노드로 나머지 두 노드를 자식 노드로 변경하는 것과 같습니다.)

4. RL 회전 (트리가 오른쪽 -> 왼쪽으로 치우쳐 있는 경우)
Step 1. 맨 하단의 노드를 가운데로 이동
Step 2. 가운데 노드를 부모 노드로 나머지 두 노드를 자식 노드로 변환
(step 1, step 2 를 묶어서 생각하면 결국 세 개의 키 값 중 가운데 값을 부모 노드로 나머지 두 노드를 자식 노드로 변경하는 것과 같습니다.)
이 네 가지 회전 방식을 한마디로 표현하면 결국 , "세 개의 키 값 중 가운데 값을 부모 노드로 나머지 두 개의 노드를 자식 노드로 바꾼다." 입니다! 쉽죠??
참고로 AVL트리 역시 이 링크를 통해 시뮬레이션해보실 수 있으니 이해가 어려우신 분들은 시뮬레이션을 사용해보셔도 좋을 것 같습니다 :)
시뮬레이션은 높이차 표현 방식이 조금 다르긴 하지만, 맥락은 같습니다!
KEY = [2, 1, 8, 9, 7, 3, 6, 4, 5]를 삽입해 보면 다음과 같이 삽입 되게 됩니다.
여기서 회전시킬 3개의 노드를 어떤 거 선택해야 하는지 헷갈릴 때가 있는데요. 3개의 노드는 높이차 2가 발생한 노드부터 삽입한 노드까지 차례대로 3개를 선택하시면 됩니다.

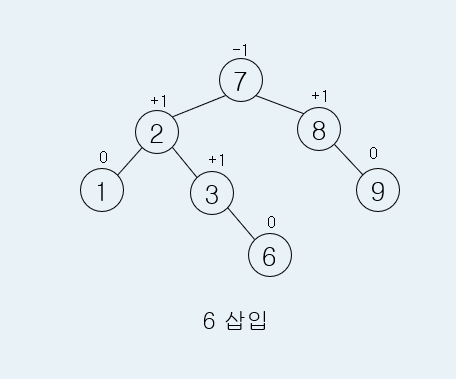


'알고리즘' 카테고리의 다른 글
| [알고리즘] DP - 스트링 편집 거리(문자열 유사도 측정) (0) | 2021.01.06 |
|---|---|
| [알고리즘] Dynamic programming (동적 계획법) 완전정복 with Python (4) | 2020.12.31 |
| [알고리즘] 탐색(2) - 레드 블랙 트리 파이썬 구현 (1) | 2020.12.05 |
| [알고리즘] 탐색(2) - 레드 블랙 트리 (0) | 2020.12.05 |
| [알고리즘] 탐색(1) - 이진 탐색, 이진 탐색 트리 with Python (0) | 2020.12.03 |
