티스토리 뷰
이진 탐색 트리의 경우 탐색에 소요되는 평균 시간 복잡도는 O(logN)이지만 최악의 경우 O(N)이 나오게 되는데요.
다음과 같이 한쪽으로 편향되어 있을 때, 즉 트리의 균형이 맞지 않을 때 탐색에 소요되는 시간이 증가하게 됩니다.
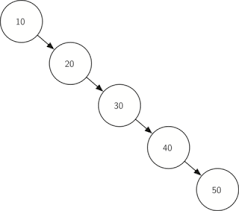
그래서 나온 것이 균형 트리(balanced tree)입니다. 균형 트리는 신규 노드 삽입시 특정 조건을 만족하도록 하여 균형 잡힌 트리를 만들어주게 됩니다.
대표적인 균형트리에는 레드-블랙트리, AVL트리 등이 있는데요. 오늘 알아볼 균형 트리는 레드-블랙 트리입니다.
레드-블랙트리는 이름에서 볼 수 있듯이 검정색 노드와 빨간색 노드를 사용하는 트리로 균형 잡힌 이진 탐색 트리라고 할 수 있습니다.
레드 블랙 트리는 신규 노드(신규 노드는 색상 레드) 삽입 시 다음과 같이 5가지의 조건을 계속 유지해야 완성이 됩니다.
1. 노드는 레드 아니면 블랙
2. 루트 노드는 블랙
3. 모든 리프 노드(말단 노드)는 블랙
-> 구현의 용이성을 위해, 모든 노드는 자식이 없는 부분에 NIL이라는 가상적인 노드를 자식으로 갖는다고 가정합니다. 결국 이 노드가 리프 노드이고 이 노드는 항상 검정색 입니다.
4. 레드 노드의 자식 노드는 항상 블랙 (레드 노드 연달아 나타날 수 없음, 블랙 노드만이 레드 노드의 부모가 될 수 있음)
5. 어떤 노드에서 리프 노드까지의 모든 경로에는 같은 수의 블랙 노드가 있음
이 5가지 조건을 유지하기 위해 노드 삽입시 회전과 색 변환이라는 두 가지 과정을 적절히 사용하는데요. 차근차근 살펴보면 별로 어렵지 않습니다!
혹시라도 이해가 어려우신 분들은 https://www.cs.usfca.edu/~galles/visualization/RedBlack.html 여기서 레드-블랙 트리 삽입 삭제 탐색 시뮬레이션이 가능하니 한번 들어가 보세요! ㅎㅎ
1. 회전
부모 노드가 레드인데, 부모 노드의 형제가 없거나 블랙일 때 수행
삽입 노드, 부모 노드, 조부모 노드 중 가운데 값을 부모로, 나머지 두 노드를 자식 노드로 변환 & 가운데 노드 검정 나머지 빨강 (다른 서브 트리에 영향 끼치지 않음)
예시)
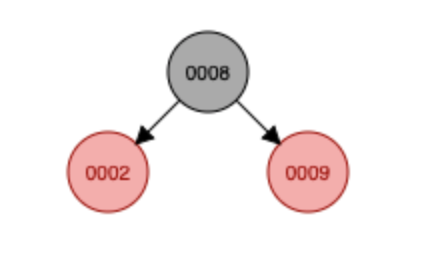
key [2, 8, 9] 삽입 시, 다음과 같이 삽입되고, 조건 4(레드 노드의 자식 노드는 항상 블랙)를 위반하게 됩니다.

따라서 회전을 통해 조건을 맞춰주게 되는데요. 각각 삽입 노드 (9) 부모 노드 (8) 조부모 노드(2)에서 가운데 값은 부모 노드 (8) 이기 때문에 부모 노드가 가운데로 오고 나머지 두 노드는 자식 노드가 됩니다.
2. 색 변환
부모 노드가 레드인데, 부모 노드의 형제가 레드일 때 수행
부모 노드& 부모 형제 노드 색상은 블랙으로, 조부모 노드 색상은 레드로 변환 (다른 서브 트리에 영향 끼칠 수 있음)
예시)
다음은 색 변환인데요. 10을 새로 삽입하게 되면 또 4번 조건을 위반하게 됩니다. 그래서 회전 또는 색변환을 해줘야 하는데, 이번엔 부모 노드의 형제가 레드이기 때문에 회전이 아닌 색변환을 해줍니다.
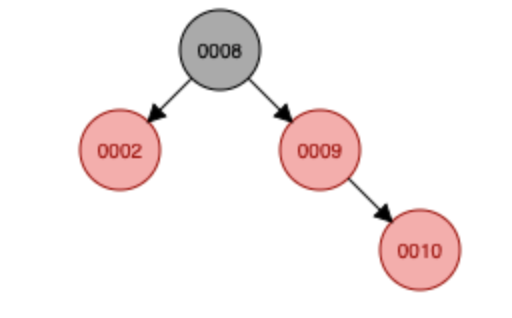
색변환 후

key가 8인 노드가 레드가 아닌 블랙인 것을 의아하게 생각할 수도 있는데요. 색변환 시 조부모 노드의 색이 레드로 전환되는 것은 맞지만, 이렇게 되면 조건 2를 위반하게 됩니다. 무조건 루트 노드는 블랙이기 때문에 레드가 아닌 블랙으로 색상을 유지해주어야 합니다.
이제 레드-블랙트리를 만들기 위한 조건과 방법을 배웠으니 실제로 적용해보겠습니다. ㅎㅎ
key = [2, 1, 8, 9, 7, 3, 6, 4, 5]
2, 1, 8 삽입

9 삽입 -> 조건 안 맞음 -> 색변환 수행
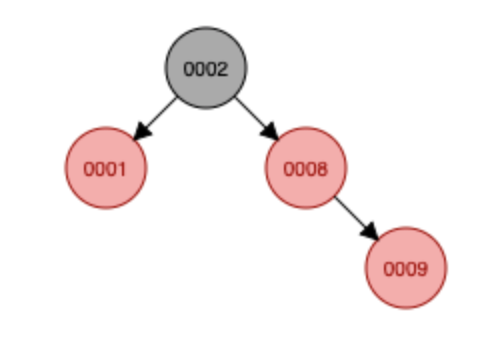
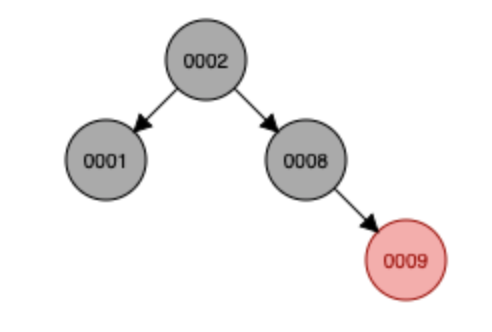
7,3 삽입 -> 3 삽입 시 조건 안 맞음 -> 색 변환 수행

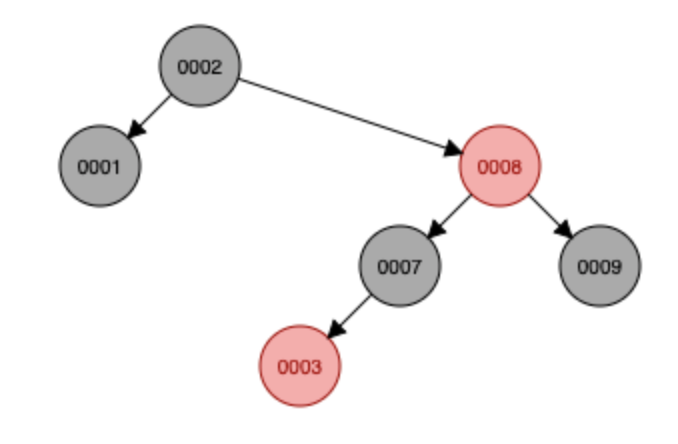
6 삽입 -> 조건 안 맞음 -> 회전 수행
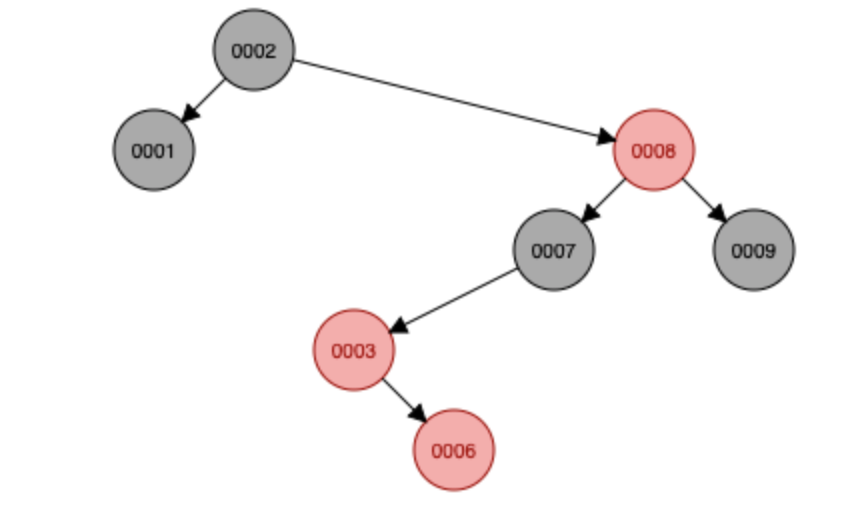

이제 4를 삽입하는데요. 조금 복잡하니 잘 따라오셔야 합니다 ㅎㅎ;
이번에는 레드-블랙트리 조건을 만족하기 위해 색변환 -> 회전 -> 회전 이렇게 세 번 일어나게 됩니다. 이렇게 연속으로 색변환 또는 회전을 하는 이유는 회전 또는 색변환의 결과가 레드-블랙트리 조건에 맞지 않기 때문입니다.


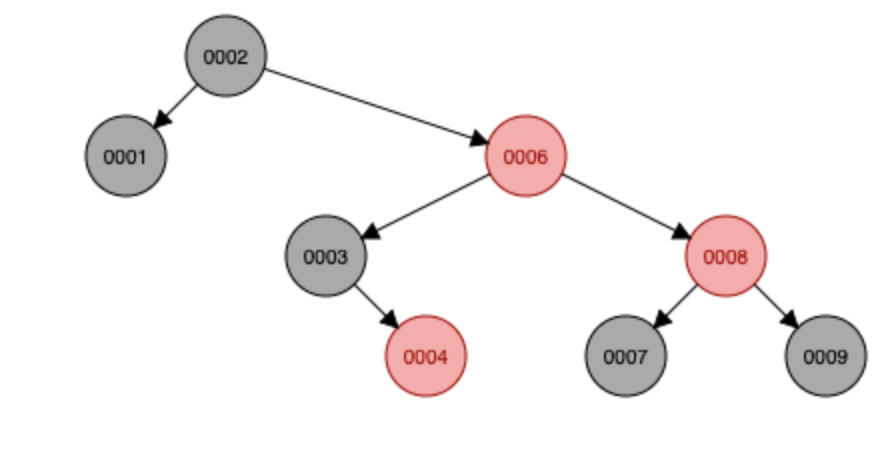

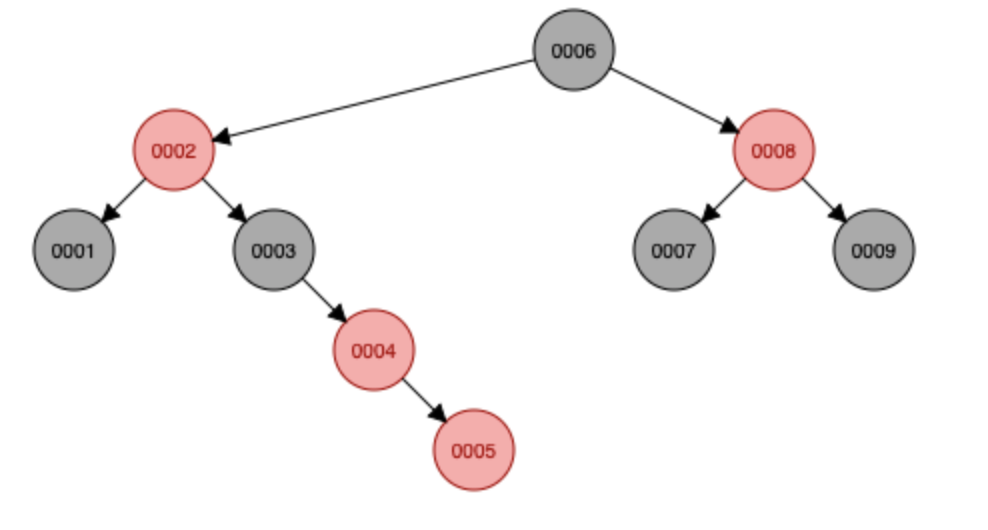
마지막으로 5 삽입~! 조건이 맞지 않기 때문에 회전을 끝으로 레드-블랙 트리가 완성되게 됩니다.

원래는 파이썬 구현 코드를 같이 작성하려 했는데 글이 너무 길어져서 다음 포스팅에 작성하겠습니다.
읽어주셔서 감사합니다 :)
'알고리즘' 카테고리의 다른 글
| [알고리즘] Dynamic programming (동적 계획법) 완전정복 with Python (4) | 2020.12.31 |
|---|---|
| [알고리즘] 탐색(3) - AVL 트리 (0) | 2020.12.06 |
| [알고리즘] 탐색(2) - 레드 블랙 트리 파이썬 구현 (1) | 2020.12.05 |
| [알고리즘] 탐색(1) - 이진 탐색, 이진 탐색 트리 with Python (0) | 2020.12.03 |
| 시간복잡도 O(NlogN)정렬 알고리즘 알아보기 with Python (0) | 2020.11.28 |
