 [알고리즘] 탐색(3) - AVL 트리
[알고리즘] 탐색(3) - AVL 트리
AVL트리 역시 레드-블랙 트리와 마찬가지로 자가 균형 이진 탐색 트리입니다. 레드-블랙 트리와 다른 점은 균형(balance)을 유지하기 위해 적용하는 조건이 다른데요. 그래서 같은 자가 균형 이진 탐색 트리이지만 같은 키를 삽입해도 트리의 결과는 다르게 나올 수 있습니다. ex) KEY = [2, 1, 8, 9, 7, 3, 6, 4, 5] 삽입 시 AVL트리 조건은 다음과 같습니다. 1. *높이 차가 2 이상이 되면 회전을 통해 높이차를 1 이하로 유지 * 높이 차 = 오른쪽 서브 트리의 높이 - 왼쪽 서브 트리의 높이 조건은 엄청 간단하죠?? 여기서 높이 차에 대해 예시를 통해 설명드리자면 각각의 노드 옆에 높이차를 적게 되는데, 이 높이 차는 해당 노드의 우측 서브 트리 높이- 왼쪽 서브 트리 높..
 [알고리즘] 탐색(2) - 레드 블랙 트리 파이썬 구현
[알고리즘] 탐색(2) - 레드 블랙 트리 파이썬 구현
레드 블랙트리 개념설명에서 이어지는 포스팅으로 레드-블랙트리 개념에 대해 잘 모르시면 이 글을 먼저 읽고 와주세요! 레드블랙 트리 파이썬 코드 class Node(): def __init__(self, data): self.data = data self.parent = self.left = self.right = None self.color = 'Red' # 신규 삽입되는 노드는 항상 빨강 class RedBlackTree: # 조부모 노드 찾기 def find_grandparent_node(self,node): if (node != None and node.parent != None): return node.parent.parent else: return None # 삼촌 노드 찾기 def find_u..
 [알고리즘] 탐색(2) - 레드 블랙 트리
[알고리즘] 탐색(2) - 레드 블랙 트리
이진 탐색 트리의 경우 탐색에 소요되는 평균 시간 복잡도는 O(logN)이지만 최악의 경우 O(N)이 나오게 되는데요. 다음과 같이 한쪽으로 편향되어 있을 때, 즉 트리의 균형이 맞지 않을 때 탐색에 소요되는 시간이 증가하게 됩니다. 그래서 나온 것이 균형 트리(balanced tree)입니다. 균형 트리는 신규 노드 삽입시 특정 조건을 만족하도록 하여 균형 잡힌 트리를 만들어주게 됩니다. 대표적인 균형트리에는 레드-블랙트리, AVL트리 등이 있는데요. 오늘 알아볼 균형 트리는 레드-블랙 트리입니다. 레드-블랙트리는 이름에서 볼 수 있듯이 검정색 노드와 빨간색 노드를 사용하는 트리로 균형 잡힌 이진 탐색 트리라고 할 수 있습니다. 레드 블랙 트리는 신규 노드(신규 노드는 색상 레드) 삽입 시 다음과 같이..
 [알고리즘] 탐색(1) - 이진 탐색, 이진 탐색 트리 with Python
[알고리즘] 탐색(1) - 이진 탐색, 이진 탐색 트리 with Python
탐색 알고리즘? - 컴퓨터에 저장된 자료를 신속하고 정확하게 찾아주는 알고리즘 이진 탐색(binary search) 정렬되어 있는 배열에서 특정한 값을 찾아내는 알고리즘으로 탐색 시간 복잡도는 O(logN) 탐색 방법: 분할-정복 방법 사용 ex) 정렬된 배열 [12,15,23,48,62,98,111,130] 에서 23을 찾는다면?? 1. 가운데 값 선택 -> 48 2. 우리가 찾고자하는 23은 48 좌측에 위치함으로 탐색범위가 12~23으로 줄어듬, 줄어든 탐색범위에서 중간 값 선택 -> 15 3. 23은 15 우측에 위치, 값은 하나만 남게 되고 이 값은 23과 일치 소스코드(파이썬) def binary_search(a:list, search_key): left, right = 0, len(a) wh..
 [자료구조] 리스트 (연결 리스트 부터 이중 연결 리스트까지)
[자료구조] 리스트 (연결 리스트 부터 이중 연결 리스트까지)
오늘 알아볼 자료구조는 리스트입니다 :) 리스트란? 순서를 가지고 일렬로 나열한 원소들의 모임으로 데이터 목록을 다루는 자료구조로 기본 연산으로는 삽입, 삭제, 탐색이 있습니다. 리스트 구현 방법 1. 배열 이용 (순차적인 메모리 공간 할당) 2. 연결 리스트 이용 (노드에 분산 저장) 리스트의 연산 init(list) - 리스트 초기화 is_empty(list) - 리스트 공백 유무 검사 is_full(list) - 리스트 포화상태 유무 검사 insert(list, pos, item) - pos 위치에 item 추가 insert_last(list, item) - 리스트 맨 끝에 item 추가 delete(list, pos) - pos 위치의 요소 제거 get_entry(list, pos) - pos 위..
 Python 자료형(list,set,dictionary) 메서드 시간복잡도 정리
Python 자료형(list,set,dictionary) 메서드 시간복잡도 정리
안녕하세요 ㅎㅎ 오늘은 알고리즘 문제풀이 시 가장 많이 사용하는 리스트(list), 집합(set), 딕셔너리(dictionary) 메서드의 시간 복잡도를 정리해보려 합니다. 본격적인 시작전에 왜 여러 자료형들의 메서드에 대한 시간 복잡도를 알아야 하는지 짚고 넘어갑시다! 보통 알고리즘 문제 풀때 리스트로 큐를 구현하시는 분들이 많으실 텐데요. 여기 큐를 pop하는 반복문을 돌려서 풀어야 하는 문제가 있다고 가정해 봅시다. 만약 리스로 큐를 구현했다면 다음과 같이 나타낼 수 있는데요. 리스트의 경우 마지막 원소를 pop하는 연산의 시간 복잡도는 O(1)이지만, 그 외의 원소를 pop할 경우 원소를 한 칸씩 당기기 때문에 시간 복잡도는 O(N)이 되게 됩니다. 결국 반복문과 중첩되니 전체적인 시간 복잡도는 ..
 [자료구조] 큐(QUEUE)를 알아보자!
[자료구조] 큐(QUEUE)를 알아보자!
큐 먼저 들어온 데이터가 먼저 나가는 자료구조 -> 선입선출(First-In First-Out) ex) 매표소 대기줄: 먼저 온 사람이 먼저 계산 종류: 선형큐, 원형 큐, 덱... enqueue: 큐의 끝에 데이터 추가 dequeue: 큐 맨 앞의 데이터 제거 & 반환 ● 큐의 연산 init(q) - 큐 초기화 is_empty(q) - 큐가 공백상태인지 검사 is_full(q) - 큐가 포화상태인지 검사 enqueue(q,e) - 큐의 끝에 데이터(e) 추가 dequeue(q) - 큐의 맨 앞 데이터 제거 및 반환 peek(q) - 큐의 맨 앞 데이터 반환 ● 선형큐(Linear Queue) 배열을 이용해 선형 큐를 구현해 보겠습니다. #include #include #define MAX_QUEUE_S..
 [자료구조] 스택(stack) 이란?
[자료구조] 스택(stack) 이란?
스택 스택(stack) - 쌓아놓은 더미, 한쪽 끝에서 자료를 넣거나 뺄 수 있는 선형 자료구조, 후입선출(Last-In First-Out)구조로 가장 최근에 들어온 데이터가 가장 먼저 나간다. push - 스택에 데이터 추가 pop - 스택에서 데이터 삭제 ● 스택의 연산 create() - 스택 생성 is_full(s) - 스택이 포화상태인지 검사 is_empty(s) - 스택이 공백상태인지 검사 push() - 스택에 데이터 추가 pop() - 스택에서 데이터 삭제 peek(s) - 요소를 스택에서 제거하지 않고 보기만 하는 연산 ● 배열을 이용한 스택 구현 배열을 이용해 스택을 구현해 봅시다 ㅎㅎ 1차원 배열을 이용해 스택을 구현할 거고, 위에 적은 연산을 각각 함수로 구현할 겁니다! #inclu..
 [자료구조] 배열, 구조체 그리고 포인터
[자료구조] 배열, 구조체 그리고 포인터
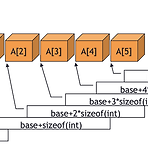
구조체 구조체(structure) - 타입이 다른 데이터를 하나로 묶는 방법 ● 구조체 선언 // 구조체 선언 struct person { char name[10]; int age; float height; }; // 구조체 변수 선언 struct person a; ● typedef를 이용한 구조체 선언 (typedef를 사용하면, 구조체 변수를 선언할 때, struct를 붙이지 않아도 됩니다.) // typedef를 이용한 구조체 선언 typedef struct person{ char name[10]; int age; float height; } person; // 구조체 변수 선언 person a; ● 자체참조 구조체 (필드 중에 자기 자신을 가리키는 포인터가 한 개 이상 존재하는 구조체) typed..
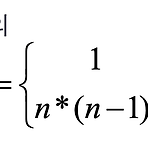 [자료구조] 순환(Recursion) with C
[자료구조] 순환(Recursion) with C
순환 순환 (재귀) - 알고리즘이나 함수가 수행 도중에 자기 자신을 다시 호출하여 문제를 해결하는 기법 예) 팩토리얼 값 구하기, 피보나치수열, 하노이 탑 등... 순환호출을 사용하여 factorial 구하기 int factorial(int n) { if(n 무한정 호출, 프로그램이 종료되지 않음 순환(recursion)과 반복(iteration)의 차이 순환 - 순환 호출 이용, 순환적인 문제에 자연스러움, 함수 호출의 오버헤드 발생 가능성 반복 - 수행속도가 빠름, 순환적인 문제에 대해서 프로그램 작성이 어려움 모든 순환은 반복으로 바꾸어 작성이 가능합니다 But!!, 매우 불편하거나 어려운 경우가 많습니다. ㅎ 순환(recursion)의 작동 원리 순환호출의 경우 복귀 주소를 시스템 스택에 저장하고..
