티스토리 뷰
스트링 편집 거리(string edit distance) 알고리즘이란 두 문자열의 유사도를 측정하기 위해 사용되는 알고리즘으로 Levenshtein distance(LD)라고도 합니다.
스트링 편집 거리 알고리즘은 논문, 보고서 등의 표절 검사, DNA 염기 서열의 유사도 검사 등에 사용되어지는데요.
두 문자열의 유사도는 S: 원래 스트링 T: 비교 스트링이라 했을 때 S -> T로 변환하는데 필요한 삽입, 삭제, 대치 연산의 최소 비용(최소 편집 횟수)을 구함으로써 판단합니다. (비용이 작게 나올수록 유사도가 큼)
만약 GUMBO라는 단어와 GAMBOL이라는 단어의 편집 거리를 구해보면, U -> A로 대치 (비용 +1), 맨 마지막에 L 추가 (비용 +1)로 편집 거리는 2가 되게 됩니다. (삽입, 삭제, 대치 비용 모두 1로 설정)
이를 MxN 행렬로 나타내서 계산해보면, 다음과 같이 나타낼 수 있습니다.

행렬의 [0][0] 인덱스의 0은 빈 문자열 로부터의 편집 거리입니다. 0을 시작으로 1,2,3,4.. 를 채워 넣게 되는데. 이는 빈 문자열을 기준으로 최소 편집 거리를 의미합니다. ex) 행렬의 [0][5] -> 5: 빈 문자열에서 'GUMBO'를 만드는데 최소 편집 비용 (삽입 5번)

같은 방식으로 두 번째 행과 두 번째 열을 채워 넣으면 위와 같이 채워 넣을 수 있습니다. ex) 행렬의 [1][4] -> 3: 문자열 'G'에서 'GUMB'를 만드는데 필요한 최소 편집 비용 (삽입: 3번)
이런 식으로 다음과 같이 행렬을 다 채워 넣으면 'GUMBO' -> 'GAMBOL'로 변환하는데 필요한 최소 편집 거리를 구할 수 있습니다.
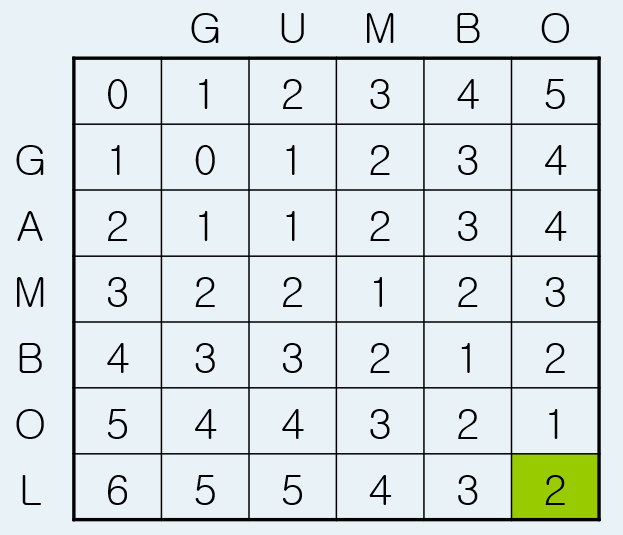
삽입, 삭제, 대치 연산 비용이 1일 때, 'GUMBO' -> 'GAMBOL'로 변환하는데 필요한 최소 편집 거리: 2
여기서, 최소 편집 거리를 구할 때 이전에 구해둔 최적 해를 사용하여 점차 더 큰 문제의 최적해를 구해나갈 수 있습니다.
점화식으로 나타내면, 다음과 같습니다. D[i,j] = min(D[i,j-1] + 삽입 비용, D[i-1,j] + 삭제비용, D[i-1,j-1] + 대치 비용) 여기서 대치 비용은 S[i] == T[j] 일 때는 0, S[i] != T[j]일 때는 1 (참고 S: 원래 스트링 T: 비교 스트링)
ex) 'GU' -> 'GA'의 최소 편집 거리를 구할 때 (행렬에서는 [3][3]), 점화식을 사용해 구해보면 min(2,2,1)로 값은 1이 나오게 됩니다.
이 점화식을 사용해 스트링 편집 거리를 다음과 같이 구현할 수 있습니다. (파이썬)
def edit_distance(s:str, t: str):
m = len(s)+1
n = len(t)+1
D = [[0]*m for _ in range(n)]
D[0][0] = 0
for i in range(1,m):
D[0][i] = D[0][i-1] + 1
for j in range(1,n):
D[j][0] = D[j-1][0] + 1
for i in range(1,n):
for j in range(1,m):
cost = 0
if s[j-1] != t[i-1]:
cost = 1
D[i][j] = min(D[i][j-1] + 1,D[i-1][j] + 1, D[i-1][j-1] + cost)
return D[n-1][m-1]
edit_distance('GUMBO', 'GAMBOL')
많은 도움이 되었길 바라며, 읽어주셔서 감사합니다!
'알고리즘' 카테고리의 다른 글
| [알고리즘] Dynamic programming (동적 계획법) 완전정복 with Python (4) | 2020.12.31 |
|---|---|
| [알고리즘] 탐색(3) - AVL 트리 (0) | 2020.12.06 |
| [알고리즘] 탐색(2) - 레드 블랙 트리 파이썬 구현 (1) | 2020.12.05 |
| [알고리즘] 탐색(2) - 레드 블랙 트리 (0) | 2020.12.05 |
| [알고리즘] 탐색(1) - 이진 탐색, 이진 탐색 트리 with Python (0) | 2020.12.03 |
